Alexander Friedmann (1888-1925) has been called the man who made the universe expand, because he first raised the possibility of the expansion of the universe (discovered later by Hubble). Friedmann was a friend of Paul Ehrenfest, from their years together in St. Petersburg. The Ehrenfest archive at the Instituut-Lorentz contains several letters and manuscripts that Friedmann sent to Ehrenfest in 1922. (This is the same archive in which the Einstein manuscripts were found.) The seminal 1922 paper is here in a Russian original, as well as an unpublished manuscript on the geometry of curved space. This material is presented here for the first time. The originals are kept in the archives of the Museum Boerhaave in Leiden. In this connection, the correspondence between Einstein and De Sitter on the nature of the Universe may be of interest as well (part of the Leiden Observatory archives). This correspondence is discussed here.

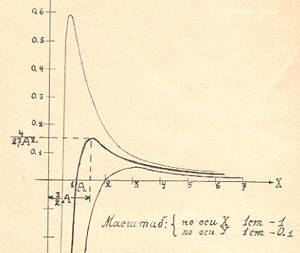
Typed manuscript О КРИВИЗНЕ ПРОСТРАНСТВА (On the curvature of space), containing handwritten formulas and corrections (dated 29 May 1922), with accompanying handwritten letter to Ehrenfest (dated 3 June 1922). A German translation Über die Krümmung des Raumes was published in Zeitschrift für Physik 10, 377 (1922). In this work Friedmann showed that Einstein’s gravitational field equations allow for an expanding universe, going against Einstein's insistence on a stationary universe. For recent English translations, see (1) and (2). To learn more about the significance of this paper for cosmology, see (1), (2), (3), (4). The final line of the Russian manuscript has been crossed out, the significance of this has been discussed by Ari Belenkiy. • Translation of Friedmann's letter to Ehrenfest (in Russian).
I'm sending you a brief note regarding the question about the possible shape of the universe more general than the cylindrical world of Einstein, and the spherical world of De Sitter; aside from these two cases there appears also a world, the space of which possesses a curvature radius varying with time; it seemed to me that a question of this sort may interest you or De Sitter. In the near future I will send you a German translation of this note, if you find the question considered in it interesting, then please be so kind to have it placed in some journal.
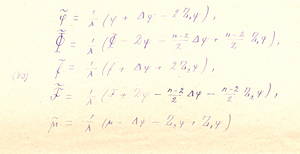
Typed manuscript К ВОПРОСУ О ГЕОМЕТРИИ КРИВЫХ ПРОСТРАНСТВ (On the question of the geometry of curved space), dated 15 April 1922, containing handwritten formulas and margin notes by Ehrenfest. This work does not appear in Friedmann's list of publications, so it seems it was never published. Ehrenfest sent this manuscript, together with a letter (undated) that Friedmann had written to Hermann Weyl, to the mathematician Jan Schouten in Delft. Schouten responded with a letter to Ehrenfest, dated 29 June 1922, in which he commented critically on Friedmann's analysis. This interaction between Friedmann and Schouten led to a joint publication in 1924 on the differential geometry of curved space [A. Friedmann and J.A. Schouten, Über die Geometrie der halbsymmetrischen Übertragungen, Mathematische Zeitschrift 21, 211 (1924).] The significance of this research towards a unified field theory is discussed here. • English translation of Friedmann's unpublished manuscript. To place this work into context, Friedmann's letter to Ehrenfest (see below) is helpful.
• Translation of Friedmann's letter to Weyl (in German).
• Translation of Schouten's letter to Ehrenfest (in Dutch).

Typed letter with handwritten conclusion, dated 15 June 1922, from Friedmann to Ehrenfest. In this letter Friedmann comments on the two papers he had just sent to Ehrenfest, the one from 15 April 1922 (On the question of the geometry of curved space) and the one from 29 May 1922 (On the curvature of space). In particular, he spells out his ideas for further research along these lines. • Translation of Friedmann's letter to Ehrenfest (in Russian).
Let me express to you my thoughts about two aspects of the modern relativity principle, and I will do so through a list of separate points split into two parts.
Carlo Beenakker
Thanks to Anton Akhmerov, Timur Galimzyanov, Sergei Mukhin, and Dmitry Pikulin for the Russian translations.