- 13.
- a.
- We hanteren dezelfde definitie van relativistische kinetische energie
Trel als in de vorige opgave, Trel=Erel-E0. Hieruit volgt Erel
=Trel+E0=2mc2+mc2=3mc2. Anderzijds,
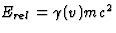 , zodat
, zodat
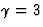 ,
, 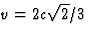 . We gebruiken hetzelfde principe als in opgave 6.
Voor de energie-impuls vectoren vóór de botsing geldt
. We gebruiken hetzelfde principe als in opgave 6.
Voor de energie-impuls vectoren vóór de botsing geldt
| 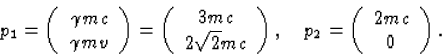 |
(28) |
Na de botsing geldt, wegens energie-impuls behoud,
| 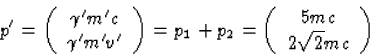 |
(29) |
Uit p'2=m'2c2 vinden we voor de massa m' van het nieuwe deeltje m'2
c2=(25-8)m2c2, ofwel 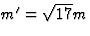 . Uit vgl. (29) lezen we nu af dat
. Uit vgl. (29) lezen we nu af dat
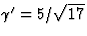 , zodat
, zodat 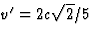 , de snelheid van het nieuwe
deeltje.
, de snelheid van het nieuwe
deeltje.
- b.
- Volkomen analoog aan de vorige opgave beginnen we met de energie-impulsvectoren
voor de botsing,
| 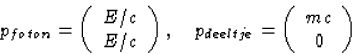 |
(30) |
(Een foton heeft energie 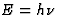 en impuls
en impuls 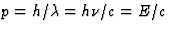 , en dus
rustmassa nul, m 2c2=E2/c2-p2=0.) Na de botsing geldt voor het nu
aangeslagen (en daardoor zwaarder geworden) deeltje
, en dus
rustmassa nul, m 2c2=E2/c2-p2=0.) Na de botsing geldt voor het nu
aangeslagen (en daardoor zwaarder geworden) deeltje
| 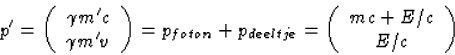 |
(31) |
De massa van het deeltje in aangeslagen toestand is nu 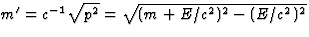
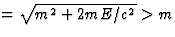 ,
,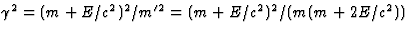 (zie vgl. (31)).
De snelheid die het deeltje krijgt is dus
(zie vgl. (31)).
De snelheid die het deeltje krijgt is dus 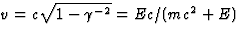 .
.
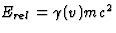 , zodat
, zodat
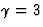 ,
, 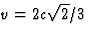 . We gebruiken hetzelfde principe als in opgave 6.
Voor de energie-impuls vectoren vóór de botsing geldt
. We gebruiken hetzelfde principe als in opgave 6.
Voor de energie-impuls vectoren vóór de botsing geldt
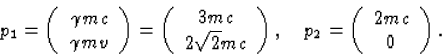
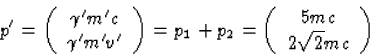
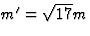 . Uit vgl. (29) lezen we nu af dat
. Uit vgl. (29) lezen we nu af dat
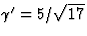 , zodat
, zodat 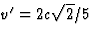 , de snelheid van het nieuwe
deeltje.
, de snelheid van het nieuwe
deeltje.
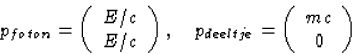
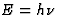 en impuls
en impuls 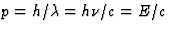 , en dus
rustmassa nul, m 2c2=E2/c2-p2=0.) Na de botsing geldt voor het nu
aangeslagen (en daardoor zwaarder geworden) deeltje
, en dus
rustmassa nul, m 2c2=E2/c2-p2=0.) Na de botsing geldt voor het nu
aangeslagen (en daardoor zwaarder geworden) deeltje
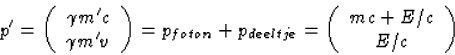
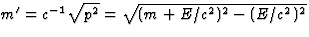
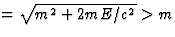 ,
,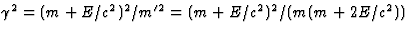 (zie vgl. (31)).
De snelheid die het deeltje krijgt is dus
(zie vgl. (31)).
De snelheid die het deeltje krijgt is dus 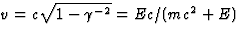 .
.