De stelling van Pythagoras zegt: het kwadraat (c2) van de
schuine zijde (c) is de som van de kwadraten
(a2+b2) van de rechte zijden (a
en b) van een rechthoekige driehoek. Of ook, de oppervlakte
(c2) van een vierkant met zijden die even lang zijn als de
schuine zijde (c), is de som van de oppervlakten
(a2+b2) van de twee vierkanten ieder met de
zijden gelijk in lengte aan een van de twee rechte zijden (a en
b). En zo hebben we bijna een bewijs van de stelling van Pythagoras
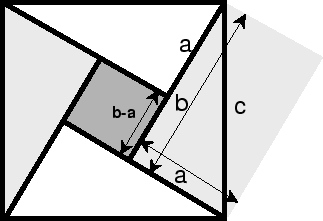
geleverd. Zie de figuur hieronder,
waar we het vierkant met oppervlak c2 opbouwen uit de
vier rechthoekige driehoeken, met schuine zijde c en rechte zijden
a en b. Daarbij houden we een vierkantje over, waarvan de
zijden een lengte b-a hebben. Omdat twee dezelfde rechthoekige
driehoeken, met hun schuine zijden tegen elkaar, een rechthoek geven met
zijden a en b en dus met een oppervlak a X b geldt dat
(c2) gelijk is aan twee maal dat oppervlak (2ab, of
ook vier maal het oppervlak van de driehoek), plus het oppervlak van het
overblijvende vierkantje ((a-b)2). Nu wat simpele algebra:
c2=2ab+(a-b)2=
2ab+a2-2ab+b2=a2+b2
en we zijn klaar met ons bewijs. De schuine zijde wordt dus gegeven door
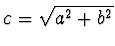
,
immers het kwadraat (c2) van de wortel is gelijk aan
a2+b2.
Terug naar de tekst.