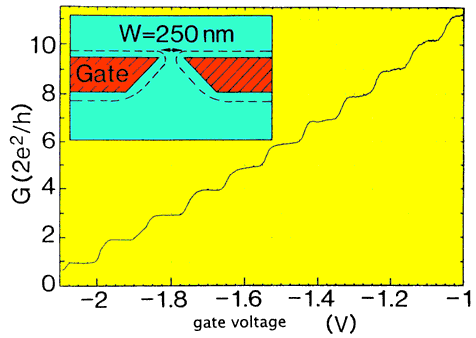
Figure 3. Quantization of the conductance of a quantum point contact. Upon increasing the width of the opening (by varying the voltage on the gate electrode shown in the inset), the conductance increases stepwise. The stepheight of 2e2/h depends only on fundamental constants of nature. [From B. J. van Wees et al., Phys. Rev. Lett. 60, 848 (1988); similar results were published by D. A. Wharam et al., J. Phys. C 21, L209 (1988).]
Now that we have discussed how a quantum billiard is fabricated, let us examine its properties in some detail. We begin with the little openings in the boundary through which the electrons enter and leave the billiard. The openings are called quantum point contacts. A special name for a hole, because it has a special property. The current of electrons through the hole is induced by application of a voltage and can be varied by adjusting the size of the opening. The bigger the opening, the bigger the current. The special property of the quantum point contact is that upon widening the opening the current does not increase gradually but stepwise. The ratio of current and voltage is the conductance. The stepwise increase of the current at a given voltage implies that the conductance can take on only discrete values. This is called the quantization of the conductance.
The term "quantization" is used in physics to indicate that some quantities can not be varied continuously, but only occur as discrete multiples of some elementary value, which is called a "quantum". We know only a few examples of quantized quantities in nature. The oldest example is the quantization of charge in multiples of the charge e of a single electron, discovered by Robert Millikan. The quantization of the magnetic flux enclosed by a superconducting ring was predicted in 1950 by Fritz London. The quantum in this case is h/2e, where h is Planck's constant. Around the same time Lars Onsager and Richard Feynman predicted the quantization of vortices in superfluid helium. A more recent quantization effect is the quantum Hall effect, discovered in 1980 by Klaus von Klitzing. The quantized conductance of a quantum point contact (shown in figure 3) was discovered in 1988 by a Dutch group (from Philips and the University of Delft) and almost simultaneously by a group in England (from the University of Cambridge).
The quantum of conductance is 2e2/h, corresponding to a resistance of 12906 Ohm. The conductance G of a quantum point contact is an integer N times the conductance quantum,
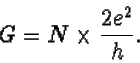
The number N is approximately equal to the width of the contact divided by half the electron wave length. The electron wave can only pass through the hole in one of a few modes of vibration, for which the interference is constructive rather than destructive. The number N counts the number of modes with constructive interference. The quantization of conductance occurs because of the equipartitioning of current among these modes: each mode carries the same current, equal to 2e2/h times the voltage.