7. Lorentz 4-vectoren

In de 3-dimensionale ruimte kennen we het begrip vector. Een vector is iets wat niet alleen een grootte heeft maar ook een richting. Een vector $\vec a$wordt dus beschreven door drie getallen, de drie componenten ax, ay, az van de vector in de richting van de drie coördinaatassen van een rechthoekig of Cartesisch ruimtelijk coördinaatsysteem met coördinaten x, y en z.

Bij overgang van één Cartesisch coördinaatsysteem C, met coördinaten x, y, en z, naar een tweede systeem C', met x', y' en z', veranderen de componenten van een vector op de dezelfde wijze als de ruimtelijke coördinaten. Stel bijvoorbeeld dat we overgaan naar een stelsel C' dat ten opzichte van C gedraaid is over een hoek $\theta$ rond de z-as. De coördinaten transformeren dan volgens
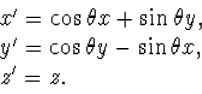\begin{displaymath} \begin{array} {l} x'=\cos\theta x+\sin\theta y,\\ y'=\cos\theta y-\sin\theta x,\\ z'=z.\end{array}\end{displaymath} (7.1)

De componenten van een vector $\vec a$ veranderen dan op dezelfde manier, nl. als
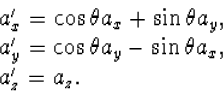\begin{displaymath} \begin{array} {l} a_x^\prime=\cos\theta a_x+\sin\theta a_y,\... ...ime=\cos\theta a_y-\sin\theta a_x,\\ a_z^\prime=a_z.\end{array}\end{displaymath} (7.2)

Een vector $\vec a$ heeft een lengte, die we soms als a of $\vert\vec a\vert$ aangeven, en die gedefiniëerd is als
\begin{displaymath} \vert\vec a\vert=\sqrt{a_x^2+a_y^2+a_z^2}.\end{displaymath} (7.3)

De lengte van een vector is in ieder Cartesisch coördinaatstelsel het zelfde; voor een draaiing zoals weergegeven in de formules (7.1) en (7.2) kunnen we dat eenvoudig verifiëren. Voor twee vectoren $\vec a$ en $\vec b$ is er een inwendig product, dat we aangeven als $\vec a\cdot\vec b$, en dat gedefiniëerd is als
\begin{displaymath} \vec a\cdot\vec b=a_xb_x+a_yb_y+a_zb_z.\end{displaymath} (7.4)

Het inwendig product, dat iets zegt over de lengte van beide vectoren en hun onderlinge hoek, is ook onafhankelijk van het gekozen Cartesisch coördinaatsysteem. Er geldt natuurlijk
\begin{displaymath} \vert\vec a\vert=\sqrt{\vec a\cdot\vec a}.\end{displaymath} (7.5)

In de niet-relativistische fysica komen veel vectorgrootheden voor; het gebruik van de bijbehorende vectornotatie maakt het mogelijk allerlei eigenschappen en relaties compact te formuleren. In de mechanica hebben we als vectoren behalve de snelheid natuurlijk ook versnelling, impuls en kracht. De plaats van een deeltje is een vector als we coördinaatstelsels met de zelfde oorsprong bekijken. In de theorie van het electromagnetisme hebben we onder meer de electrische veldsterkte.

Opmerking: Behalve vectoren zijn er ook pseudo-vectoren. Hierbij komt er een extra minteken voor de componenten als we naar een gespiegeld coördinatenstelsel overgaan, bijvoorbeeld x'=-x, y'=-y, z'=-z, of x'=-x, y'=y, z'=z. In de mechanica is het impulsmoment van een deeltje ten opzichte van een vaste oorsprong een pseudo-vector; in het electromagnetisme hebben we de magnetische veldsterkte als pseudo-vector. In dit inleidend college zullen we ruimtespiegelingen buiten beschouwing laten. We hoeven dan geen onderscheid te maken tussen vectoren en pseudo-vectoren, en mogen het impulsmoment en de magnetische veldsterkte als vectoren opvatten.

De tot nu toe gebruikte aanduiding voor de drie assen van rechthoekige ruimtelijke coördinaatstelsels en voor de daarbij behorende componenten van vectoren is niet erg handig, als we maximaal willen profiteren van de mogelijkheden tot compacte formuleringen, die het vectorbegrip ons biedt. Dit is vooral duidelijk bij formules waarin er over componenten gesommeerd moet worden. We zullen daarom van nu af rechthoekige ruimtelijke coördinaten niet meer aangeven als x, y en z, maar als x1, x2 en x3. Deze coördinaten horen dus bij de x1-, x2- en x3-as. De componenten van een vector $\vec a$ zullen we a1, a2 en a3 noemen. We kunnen dan de lengte van een vector $\vec a$ en het inwendig product van een vector $\vec a$ met een vector $\vec b$ met behulp van sommatietekens wat korter schrijven als
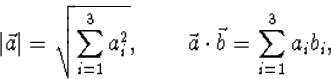\begin{displaymath} \vert\vec a\vert=\sqrt{\sum_{i=1}^3a_i^2},\qquad\vec a\cdot\vec b= \sum_{i=1}^3a_ib_i,\end{displaymath} (7.6)

De formules die de relaties tussen twee Cartesische coördinaatsystemen beschrijven worden matrixformules. Zo schrijven we (7.1) en (7.2) als
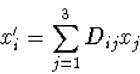\begin{displaymath} x_i^\prime=\sum_{j=1}^3D_{ij}x_j\end{displaymath} (7.7)

en
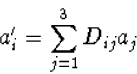\begin{displaymath} a_i^\prime=\sum_{j=1}^3D_{ij}a_j\end{displaymath} (7.8)

waarbij de Dij de elementen zijn van de 3 X 3 matrix
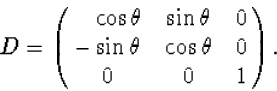\begin{displaymath} D=\pmatrix{\hphantom{-}\cos\theta&\sin\theta&0\cr -\sin\theta&\cos\theta& 0\cr0&0&1\cr}.\end{displaymath} (7.9)

Een draaiing over een willekeurige hoek en om een willekeurige as - dus niet noodzakelijk één der coördinaatassen - kan op deze manier met behulp van een geschikte 3 X 3 matrix worden beschreven. Onder zo'n draaiing blijft de lengte van de coördinaatvector onveranderd, d.w.z. er geldt
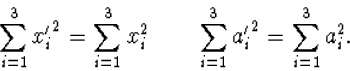\begin{displaymath} \sum_{i=1}^3{x_i^\prime}^2=\sum_{i=1}^3 x_i^2\qquad \sum_{i=1}^3{a_i^\prime}^2=\sum_{i=1}^3 a_i^2.\end{displaymath} (7.10)

Omgekeerd kan men nagaan dat iedere lineaire transformatie x1, x2, x3 $\rightarrow$ x1', x2', x3', die deze eigenschap heeft een draaiing is, of een draaiing gevolgd door een spiegeling. Men noemt zo'n transformatie wel een orthogonale transformatie, en de 3 X 3 matrix Dij, die er volgens formule (7.7) bijhoort, een orthogonale matrix.

Opmerkingen:

Eén van de leidende ideeën van de relativiteitstheorie is dat gebeurtenissen beschreven kunnen worden als punten van een 4-dimensionale ruimte, de ruimte-tijd. We gaan daarom in deze 4-dimensionale ruimte een aantal begrippen invoeren, die analoog zijn aan begrippen die we kennen van de gewone 3-dimensionale ruimte, en die we in het voorafgaande kort hebben samengevat. De voordelen zullen de zelfde zijn: compacte schrijfwijze van belangrijke relaties en formules. We beginnen ook hier met een betere notatie. We gebruiken natuurlijk x1, x2 en x3 in plaats van x, y en z voor de ruimtelijke coördinaten van een gebeurtenis. Als vierde coördinaat nemen we niet de tijd t zelf, maar t vermenigvuldigd met de constante lichtsnelheid c. Deze vierde coördinaat noemen we x0, dus x0=ct. Het voordeel van deze keuze is dat de vier coördinaten op deze manier de zelfde dimensie hebben, nl. de dimensie van een lengte. We schrijven dan voor een punt in de 4-dimensionale ruimte
\begin{displaymath} \underline{x}=(x_0,x_1,x_2,x_3).\end{displaymath} (7.11)

Let daarbij op de volgorde die we gekozen hebben. Merk ook op dat de schrijfwijze $\underline{x}$, die we om practische redenen in dit college zullen gebruiken, géén standaardnotatie is. Meestal schrijft men voor het viertal gewoon x, maar dat hadden we hier al gebruikt voor de lengte van $\vec x$. Een andere gewoonte is de vier coördinaten aan te geven als $x_\mu$ (of als $x^\mu$), waar bij de griekse index wordt geacht de waarden 0,1,2 en 3 aan te nemen, terwijl latijnse indices geacht worden de waarden 1,2 en 3 aan te nemen (dus alleen voor ruimtelijke componenten).

De nieuwe manier om ruimte-tijd coördinaten aan te geven maakt het mogelijk de Lorentz transformaties, die optreden als we van een gegeven inertiaalsysteem S overgaan naar een ander inertaalsysteem S', in een compacte matrixvorm te schrijven, net zo als we dat hier boven met de orthogonale transformaties in de Cartesische ruimte hebben gedaan. De standaard Lorentz transformatie in de x1-richting van formule (4.37) wordt dan
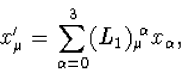\begin{displaymath} x_\mu^\prime=\sum_{\alpha=1}^4(L_1)_\mu{\!}^\alpha x_\alpha,\end{displaymath} (7.12)

met daarin de 4 X 4 matrix $(L_1)_\mu{\!}^\alpha$ gegeven als
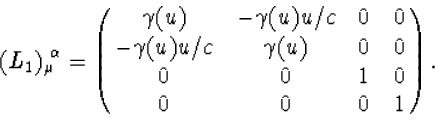\begin{displaymath} (L_1)_\mu{\!}^\alpha=\pmatrix{\gamma(u)&-\gamma(u)u/c&0&0\cr -\gamma(u)u/c&\gamma(u)&0&0\cr0&0&1&0\cr0&0&0&1\cr}.\end{displaymath} (7.13)

Let op de gevolgen van het feit dat we de tijdcoördinaat x0=ct voorop gezet hebben. Ook hebben we bij het aangeven van de indices van de matrix L1 de rechter index boven gezet. Dit is niets meer dan een notatie kwestie. We zullen verderop uitleggen waarvoor dit handig is.

Op dezelfde manier schrijven we ook de standaard Lorentz transformaties in de x2 en x3 richting van formules (4.39) en (4.40) met matrices $(L_2)_\mu{\!}^\alpha$ en $(L_3)_\mu{\!}^\alpha$, die we uit deze formules kunnen aflezen, en die gelijk zijn aan
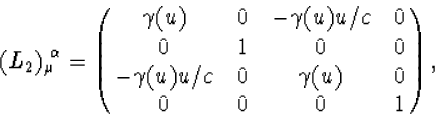\begin{displaymath} (L_2)_\mu{\!}^\alpha=\pmatrix{\gamma(u)&0&-\gamma(u)u/c&0\cr 0&1&0&0\cr-\gamma(u)u/c&0&\gamma(u)&0\cr0&0&0&1\cr},\end{displaymath} (7.14)

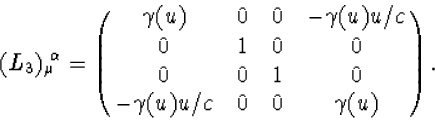\begin{displaymath} (L_3)_\mu{\!}^\alpha=\pmatrix{\gamma(u)&0&0&-\gamma(u)u/c\cr... ...cr0&0&1&0\cr-\gamma(u)u/c&0&0&\gamma(u)\vspace{-4mm}\cr&&&\cr}.\end{displaym ath} (7.15)

Ook algemene Lorentz transformaties zoals besproken in Hoofdstuk 5 kunnen op deze manier worden geschreven met behulp van een 4 X 4 matrix L.

Merk op dat de inverse van een Lorentz transformatie met matrix L door de inverse matrix L-1 wordt beschreven. Als we met behulp van de matrix L' van één inertiaalsysteem S naar een tweede inertiaalsysteem S' overgaan, en vervolgens met de matrix L naar een derde systeem S'', kunnen we het totale resultaat beschrijven met de matrix LL', het matrixproduct van L en L', met matrixelementen
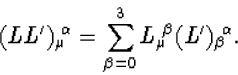\begin{displaymath} (LL')_\mu{\!}^\alpha=\sum_{\beta=0}^3L_\mu{\!}^\beta (L')_\beta{\!}^\alpha.\end{displaymath} (7.16)

We definiëren nu algemeen een Lorentz 4-vector als een grootheid met 4 componenten die bij de overgang naar een ander inertiaalsysteem op dezelfde manier transformeren als de ruimte-tijd coördinaten x0, x1, x2 en x3. (Merk even op dat we toch maar ruimte-tijd blijven zeggen, ondanks de volgorde van x0, x1, x2, x3.) We zullen zulke 4-vectoren aangeven als $\underline{a}$, $\underline{b}$, $\cdots$, met $\underline{a}=(a_0,a_1, a_2,a_3)$, $\underline{b}=(b_0,b_1,b_2,b_3)$, $\cdots$, etc. Bij een transformatie van de ruimte-tijd coördinaten $\underline{x}\rightarrow \underline{x}'$ volgens
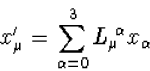\begin{displaymath} x_\mu^\prime=\sum_{\alpha=0}^3L_\mu{\!}^\alpha x_\alpha\end{displaymath} (7.17)

hoort dus een transformatie van de componenten $\underline{a}\rightarrow \underline{a}'$ volgens
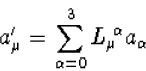\begin{displaymath} a_\mu^\prime=\sum_{\alpha=0}^3L_\mu{\!}^\alpha a_\alpha\end{displaymath} (7.18)

Als we ons beperken tot inertiaalsystemen die de zelfde oorsprong hebben, kunnen we de ruimte-tijd coördinaten van een gebeurtenis zelf ook opvatten als de componenten van een Lorentz 4-vector; in het algemenere geval vormen de verschillen van de coördinaten van twee gebeurtenissen een 4-vector.

We definiëren het inwendig product van twee 4-vectoren $\underline{a}$ en $\underline{b}$ als
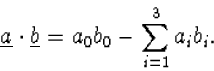\begin{displaymath} \underline{a}\cdot\underline{b}=a_0b_0-\sum_{i=1}^3a_ib_i.\end{displaymath} (7.19)

Dit inwendig product is verschillend van het 3-dimensionale inwendig product in (7.6). Dit laatste is positief definiet: $\vec a\cdot\vec a$ is groter of gelijk aan nul; uit $\vec a\cdot\vec a=0$ volgt bovendien $\vec a= \vec 0$. Vanwege het minteken in (7.18) is dit niet meer het geval voor het 4-dimensionale inwendige product.

Het inwendig product in de ruimte-tijd is indefiniet: $\underline{a}\cdot\underline{a}$ kan negatief zijn; bovendien kan $\underline{a}\cdot\underline{a}$ nul zijn zonder dat de 4-vector $\underline{a}$ zelf nul is.

We laten nu zien waarom men voor Lorentz 4-vectoren dit inwendig product heeft gekozen, en niet een definiet positief inwendig product met alleen plustekens. Bekijk het inwendig product van de ruimte-tijd 4-vector $\underline{x}=(x_0,x_1,x_2,x_3)$ met zich zelf. Dit is gelijk aan
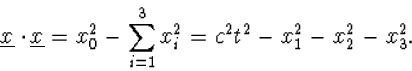\begin{displaymath} \underline{x}\cdot\underline{x}=x_0^2-\sum_{i=1}^3x_i^2= c^2t^2-x_1^2-x_2^2-x_3^2.\end{displaymath} (7.20)

Dit is niets anders dan de fundamentele kwadratische vorm, die we in het begin van hoofdstuk 5 hebben ingevoerd, en verder in hoofdstuk 6 hebben gebruikt om allerlei belangrijke fysische eigenschappen van de ruimte-tijd te karakteriseren. Deze kwadratische vorm was invariant onder standaard Lorentz transformaties. Dit hing direct samen met het belangrijke fysisch gegeven dat de lichtsnelheid het zelfde was in alle inertiaalsystemen. We hebben in hoofdstuk 5 de invariantie van de kwadratische vorm in feite gebruikt om algemene Lorentz transformaties mee te definiëren.

Uit de invariantie van $\underline{x}\cdot\underline{x}$ kan men gemakkelijk afleiden dat ook $\underline{x}\cdot\underline{y}$, het inwendig product van twee ruimte-tijd 4-vectoren $\underline{x}=(x_0,x_1,x_2,x_3)$ en $\underline{y}=(y_0,y_1,y_2,y_3)$, invariant is onder Lorentz transformaties. Bekijk daartoe de inwendige producten van $\underline{x}+\underline{y}$ en $\underline{x}-\underline{y}$ met zich zelf. Beide zijn natuurlijk Lorentz invariant. Met de bilineariteit van het inwendig product schrijven we
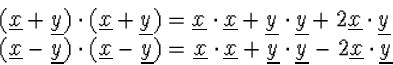\begin{displaymath} \begin{array} {l} (\underline{x}+\underline{y})\cdot(\underl... ...\cdot\underline{y}-2\underline{x}\cdot \underline{y}\end{array}\end{displaymath} (7.21)

en dus
\begin{displaymath} \underline{x}\cdot\underline{y}=\{ (\underline{x}+\underline... ...erline{x}-\underline{y})\cdot(\underline{x}-\underline{y})\}/4.\end{displaymath} (7.22)

Daaruit volgt dat $\underline{x}\cdot\underline{y}$ Lorentz invariant is voor willekeurige $\underline{x}$ en $\underline{y}$. Voor de componenten van de ruimte-tijd 4-vectoren $\underline{x}$ en $\underline{y}$ kunnen we 8 willekeurige getallen nemen. Voor twee Lorentz 4-vectoren $\underline{a}$ en $\underline{b}$ kunnen we dat ook doen. Beide stellen van 8 getallen transformeren op de zelfde manier als we met een Lorentz transformatie naar een ander inertiaalsysteem overgaan. Daaruit kunnen we een belangrijke conclusie trekken:

Het inwendig product $\underline{a}\cdot\underline{b}$van twee willekeurige Lorentz 4-vectoren $\underline{a}$ en $\underline{b}$is invariant onder Lorentz transformaties.

De 4-dimensionale ruimte-tijd voorzien van het inwendig product
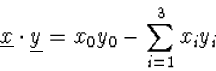\begin{displaymath} \underline{x}\cdot\underline{y}=x_0y_0-\sum_{i=1}^3x_iy_i \end{displaymath} (7.23)

en de daar bij behorende kwadratische vorm
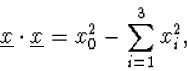\begin{displaymath} \underline{x}\cdot\underline{x}=x_0^2-\sum_{i=1}^3x_i^2, \end{displaymath} (7.24)

wordt wel Minkowski-ruimte genoemd.

We merken nog op dat het invariante inwendige procuct (kortweg ook wel inproduct genoemd) van twee 4-vector $\underline{x}$ en $\underline{y}$gegeven wordt door
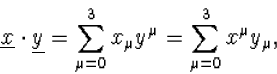\begin{displaymath} \underline{x}\cdot\underline{y}=\sum_{\mu=0}^3 x_\mu y^\mu=\sum_{\mu=0}^3 x^\mu y_\mu,\end{displaymath} (7.25)

indien we de notatie van een bovenindex hebben ingevoerd,
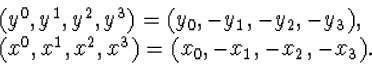\begin{displaymath} \begin{array} {l} (y^0,y^1,y^2,y^3)=(y_0,-y_1,-y_2,-y_3),\\ (x^0,x^1,x^2,x^3)=(x_0,-x_1,-x_2,-x_3) .\end{array}\end{displaymath} (7.26)

Bij het vormen van een inwendig product sommeert men dus over de componenten van de twee 4-vectoren, waarbij de ene 4-vector de index boven en de andere de index beneden heeft (vergelijk de notatie voor de 4 X 4 matrix L behorende bij een Lorentz transformatie). Zo'n sommatie komt zo vaak voor dat ik U niet wil onthouden wat Einstein wel gekscherend zijn belangrijkste ontdekking heeft genoemd, namelijk de sommatieconventie.

De sommatieconventie: over twee gelijke indices, waarvan een boven en een onder, wordt automatisch gesommeerd.

Dit voorkomt veel schrijfwerk en het verdient de voorkeur in de paar gevallen dat sommatie niet plaats dient te vinden, dit expliciet te vermelden. In het geval van de 3-dimensionale Cartesische ruimte is de lengte van een vector $\vec a$ gelijk aan de wortel van het inwendig product van die vector met zich zelf. Voor een Lorentz 4-vector $\underline{a}$ kan het inwendig product negatief zijn. In dat geval moet men de ``lengte'' van $\underline{a}$zorgvuldiger definiëren. In aansluiting op wat we in hoofdstuk 6 besproken hebben, onderscheiden we de volgende gevallen:

Tijdachtige en lichtachtige 4-vectoren hebben dus een ``lengte'' $\vert\underline{a}\vert=\sqrt{\underline{a}\cdot\underline{a}}$, maar voor ruimteachtige 4-vectoren moeten we kennelijk $\vert\underline{a}\vert=\sqrt{-\underline{a}\cdot\underline{a}}$ definiëren. Omdat $\underline{a}\cdot\underline{a}$ en het teken van dit inwendig product onafhankelijk is van het stelsel waarin we het bepalen - het is invariant onder Lorentz transformaties - is voor een ruimteachtige 4-vector aldus de lengte welgedefiniëerd.

Een lichtachtige vector volgt altijd een lichtstraal. Het is een fundamenteel uitgangspunt van de relativiteitstheorie dat dit in ieder stelsel het geval is (het lichtpostulaat). Even fundamenteel is dat voor een tijdachtige vector er altijd een inertiaalstelsel te vinden is waarvoor de ruimtelijke componenten van de 4-vector gelijk aan nul zijn. Evenzo kan voor een ruimteachtige vector $\underline{a}$ altijd een stelsel gevonden worden waarvoor de tijdscomponent gelijk aan nul is. In zo'n stelsel kan men met recht over de lengte van de vector spreken ($\vert\vec a\vert$), die dus in een willekeurig stelsel gedefinieerd kan worden door $\sqrt{-\underline{a}\cdot\underline{a}}$.

Opgave 19:

Geef een bewijs van de uitspraken gedaan in bovenstaande paragraaf.

Uit de bespreking van het Doppler-effect is eenvoudig af te leiden dat we met golfvector en cirkelfrequentie een 4-vector kunnen samenstellen. Transformatie regels werden afgeleid door te eisen dat $\vec k\cdot\vec x-\omega t$ onveranderd blijft onder een Lorentz transformatie.

Opgave 20:

Laat zien dat $\underline{k}=(\omega/c,k_x,k_y,k_z)$ transformeert als een 4-vector onder Lorentz transformaties.

Hiermee hebben we dus naast het voorbeeld van de punten in de ruimte-tijd een ander expliciet voorbeeld van een Lorentz 4-vector. De golf-4-vector speelt een belangrijke rol, omdat uit vele experimenten, al voor de formulering van de relativiteitstheorie, bekend was dat licht naast een golfkarakter ook een deeltjeskarakter heeft. Het bijbehorende deeltje werd een foton genoemd. Hoewel het niet tot stilstaan gebracht kan worden (immers de lichtsnelheid is in ieder stelsel gelijk aan c), manifesteert het zich wel als een deeltje met een energie $E=h\nu=\hbar\omega$ en een impuls $\vec p=\hbar\vec k$. Impuls is hoeveelheid beweging, en voor een deeltje met massa m wordt het gegeven door $\vec p=m\vec v$. In het volgende hoofdstuk zullen we dit uitvoerig bespreken. Verder is $\hbar=h/(2\pi)$ en h de constante van Planck, h=6,626 X 10-34kg m2/s. Deze had h ingevoerd om tot een correcte beschrijving van de thermische straling te komen. Einstein heeft h in zijn bestudering van het fotoelectrische effect geïnterpreteerd als de constante die nodig is om te verklaren dat licht dat op een kathode valt slechts electronen met een heel bepaalde energie ($E=h\nu$) vrijmaakt. Het was hiervoor, en niet voor de relativiteitstheorie, dat Einstein in 1922 de Nobelprijs kreeg. De stralingsdruk kon nu gezien worden als de impulsoverdracht door deze lichtdeeltjes (een lichtbundel kan gezien worden als een stroom van lichtdeeltjes). Deze impuls is precies $\hbar\vec k$ (in grootte dus gelijk aan $h/\lambda$). Om de overeenkomsten en de verschillen tussen de gebruikelijke 3-vectoren en de in dit hoofdstuk ingevoerde Lorentz 4-vectoren goed te begrijpen geven we nog een overzicht.

Overzicht:

In de 3-dimensionale ruimte gebruiken we Cartesische coördinaatstelsels.        In de 4-dimensionale ruimte-tijd gebruiken we inertiaalstelsels.
          
Alle Cartesische coördinaatsystemen zijn equivalent wat hun fysische betekenis betreft (isotropie van de ruimte).        Alle inertiaalsystemen zijn fysisch equivalent (het relativiteitsprincipe).
          
Ze zijn onderling verbonden door orthogonale transformaties (draaiingen en spiegelingen).        Ze zijn onderling verbonden door Lorentz transformaties.
          
Er is een positief definiet inwendig product, waar mee de lengte van een vector gedefiniëerd kan worden.        Er is een indefiniet inwendig product, dat voor tijdachtige en ruimteachtige 4-vetoren een ``lengte'' definiëert.
          
Het inwendig product en de daarvan afgeleide lengte zijn invariant onder orthogonale transformaties.        Het inwendig product en de daarvan eventueel afgeleide ``lengte'' zijn invariant onder Lorentz transformaties.

  • Volgende hoofdstuk
  • Naar inhoudsopave