Speciale Relativiteitstheorie - opgaven voor 5-6 VWO klassen
We hebben gezien dat de uitgangspunten van Einstein's
relativiteitstheorie verrassend eenvoudig zijn. Met weinig middelen kan je zelf
al heel leuke resultaten behalen. Voor de hier volgende opgaven 1 en 2 is
slechts het constant zijn van de lichtsnelheid (die we altijd c noemen)
nodig. In opgave 3 is ook nog de Lorentzcontractie (het feit dat voor een
bewegende waarnemer voorwerpen in de lengterichting verkort lijken) nodig.
Noem L0 de lengte die de waarnemer meet als een voorwerp
in rust is ten opzichte van de waarnemer. Als het voorwerp niet in rust is
t.o.v de waarnemer, meet deze een lengte L, gegeven door
Hier is v de relatieve snelheid van het voorwerp t.o.v. de waarnemer.
Veel plezier met de opgaven!
1. Het "optellen" van snelheden
De niet-relativistische manier van het (letterlijk) optellen van snelheden
kan niet goed zijn, omdat deze kan leiden tot snelheden die groter zijn
dan de lichtsnelheid. Hoe moet het dan wel? Om daar achter te komen voeren we
een gedachtenexperiment uit (bedacht door N.D. Mermin).
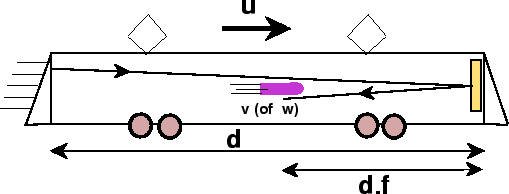
We stellen ons een trein voor, rijdend met snelheid u (t.o.v. een
waarnemer). Vanuit één kant (de linkerkant in het plaatje) van de
trein worden tegelijkertijd een kogel (met snelheid w t.o.v. een
waarnemer) en een lichtflits naar de andere kant geschoten. De lichtflits is
natuurlijk sneller aan de andere kant dan de kogel, en wordt daar gereflecteerd
in een spiegel. Op de weg terug komt de lichtflits de kogel tegen op een
bepaalde fractie f van de lengte van de trein (die we d zullen
noemen). Belangrijk is nu dat voor alle waarnemers f hetzelfde is;
alhoewel verschillende waarnemers van mening zullen verschillen over de lengte
d van de trein, zullen ze het er over eens zijn dat de kogel en
lichtflits elkaar ontmoeten op een specifieke fractie van die lengte. We gaan
nu f berekenen.
- a.
- We gaan eerst uit van de waarnemer buiten de trein. Noem de tijd die de
lichtflits er voor nodig heeft om de spiegel te bereiken T1.
In deze tijd heeft de lichtflits een afstand cT1 afgelegd.
Anderzijds heeft de lichtflits de lengte van de trein afgelegd, plus de afstand
die de spiegel is verplaatst in de tussentijd t.g.v. de snelheid van de trein.
De totale afstand kan dus ook worden uitgedrukt in d, u en
T1. Doe dit.
- b.
- Noem de tijd die de lichtflits er voor nodig heeft om vanaf de
spiegel de kogel te bereiken T2. In deze tijd is de afstand
fd afgelegd, verminderd met de afstand die de trein is tegemoet gekomen
in de tijd T2. Laat nu zien dat de verhouding
T2/T1 niet van d afhangt.
- c.
- De afstand die de kogel heeft afgelegd in de tijd
T1+T2, is precies gelijk aan de afstand die
de lichtflits aflegt in een tijd T1, verminderd met
de afstand afgelegd in de tijd T2. Ook hieruit is
T2/T1 te vinden. Leidt nu af dat de fractie
f gegeven wordt door
- d.
- We hebben benadrukt dat f hetzelfde is voor alle waarnemers.
In het bijzonder zal een waarnemer die met de trein meereist, vinden dat de
trein stilstaat t.o.v. hem (u=0), terwijl de kogel met een snelheid
v t.o.v. hem beweegt, en dus dat
f = (c-v)/(c+v) (controleer dit!). Laat nu
zien dat de snelheid w (die volgt uit het "optellen" van u en
v) van de kogel in de trein wordt gegeven door
Dit is het goede resultaat! Bestudeer deze formule: Wat is de w als:
u of v nul is; u of v gelijk aan de lichtsnelheid
c is; als u en v klein zijn t.o.v. c?
2. Superluminale snelheden
Volgens de relativiteitstheorie kan niets sneller gaan dan het licht. Toch heb
je misschien wel eens gehoord of gelezen dat astronomen soms objecten meten met
snelheden groter dan de snelheid van het licht (zgn. superluminale snelheden).
Is dat niet in strijd met de relativiteitstheorie?
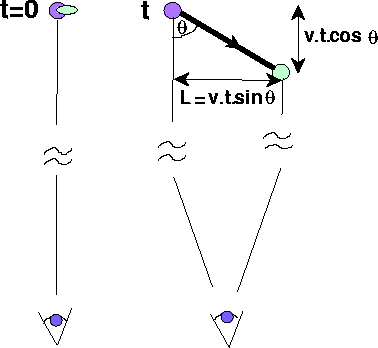
We beschouwen een verweggelegen quasar, die op een tijdstip t=0 een
gaswolk uitstoot. De snelheid van de gaswolk noemen we v, en de afstand
van de quasar tot de aarde noemen we d. De richting waarin de gaswolk
wordt uitgestoten, maakt een hoek 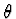 met de gezichtslijn.
met de gezichtslijn.
- a.
- Op welk tijdstip ziet een waarnemer op aarde de uitstoot van de gaswolk?
Na een tijd t is de gaswolk een afstand vt verplaatst, waarvan
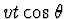 in de richting van de waarnemer, en
in de richting van de waarnemer, en 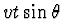 in de richting loodrecht op de gezichtslijn. Op welk tijdstip bereikt het licht
van de gaswolk op dit punt, de aarde?
in de richting loodrecht op de gezichtslijn. Op welk tijdstip bereikt het licht
van de gaswolk op dit punt, de aarde?
- b.
- De transversale snelheid vobs (dat is de snelheid
loodrecht op de lijn van waarneming), zoals die wordt waargenomen op aarde, is
de afstand loodrecht op de lijn van waarneming die de gaswolk aflegt (in een
tijd t), gedeeld door het tijdsverschil tussen de waarneming van het
uitstoten van de gaswolk en de waarneming van de gaswolk nadat deze de afstand
vt heeft afgelegd. Laat zien dat deze snelheid wordt gegeven door
Is dat groter of kleiner dan de werkelijke transversale snelheid 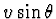 ? Kun je een
? Kun je een 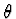 en v vinden waarvoor
vobs groter is dan de lichtsnelheid?
en v vinden waarvoor
vobs groter is dan de lichtsnelheid?
- c.
- Neem v vast, en bekijk vobs als functie van
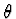 . vobs is maximaal als
. vobs is maximaal als
(probeer dit af te leiden). Laat zien dat in dat geval geldt
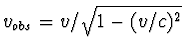
.
Hoe groot moet v minstens zijn om te zorgen dat
vobs groter is dan de lichtsnelheid?
- d.
- Waarom is dit niet in strijd met de relativiteitstheorie?
3. Voorwerpen waargenomen bij hoge snelheden
De Lorentzcontractie zegt dat voor een bewegende waarnemer voorwerpen in de
lengterichting van zijn beweging korter zijn. Equivalent: voor een stilstaande
waarnemer zijn bewegende voorwerpen korter. Je zou nu misschien denken dat als
een voorwerp een hoge snelheid heeft, je het vervormd ziet, omdat het in de
lengterichting korter wordt, maar in andere richtingen niet. De werkelijkheid
is echter iets subtieler.
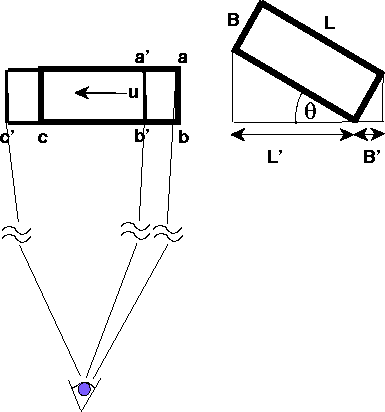
- a.
- We beschouwen een rechthoekig blok zoals aangegeven links in het
plaatje. Het blok beweegt op grote afstand van een waarnemer, met een snelheid
u. Aangegeven zijn de hoekpunten a, b en c. Op een
iets latere tijd (die we dadelijk zullen specificeren) zijn de hoekpunten
verplaatst naar a', b' en c'. Kijk nu naar de punten
b' en c'. In het ruststelsel van het blok liggen deze een lengte
L uit elkaar. Wat is de afstand tussen b' en c' die de
waarnemer ziet? Kijk nu naar het punt a'. Dit punt ligt verder weg dan
b' en c'. Het licht van dit punt zal dus langer onderweg zijn
dan dat uit b' en c'. Hoeveel langer (de afstand van a'
tot b' noemen we B)? Dit betekent dat we het licht uit punt
a' niet tegelijkertijd met dat uit b' en c'
zullen ontvangen! In plaats daarvan ontvangen we tegelijkertijd met licht uit
b', c' het licht uit een punt a dat verschoven ligt t.o.v
a. De verschuiving is gelijk aan de snelheid van het blok,
vermenigvuldigd met de tijd die het licht erover doet om de breedte van het
blok over te steken. Beschrijf nu hoe het blok door de waarnemer wordt
waargenomen.
- b.
- Beschouw nu een stilstaand blok, dat geroteerd is over een
hoek
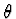 (zie rechter plaatje). Een waarnemer kijkt vanaf dezelfde
richting als onder onderdeel a tegen het blok aan. Hoe neemt hij het blok waar?
(zie rechter plaatje). Een waarnemer kijkt vanaf dezelfde
richting als onder onderdeel a tegen het blok aan. Hoe neemt hij het blok waar?
- c.
- Vergelijk de situaties van de onderdelen a en b. Als het goed is zie
je een opmerkelijke overeenkomst: de waarnemer ziet in de situatie onder a iets
vergelijkbaars als onder b! De situaties zijn zelfs precies identiek als we de
snelheid u in onderdeel a relateren aan de hoek
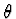 onder b.
Geef deze relatie.
onder b.
Geef deze relatie.
- d.
- Denk nu eens na hoe diverse objecten eruit zien als ze worden
waargenomen met een hoge snelheid. Denk bijvoorbeeld aan een bol (zoals een
doorzichtige gasnevel), of een platte ronde schijf, onder diverse hoeken met de
bewegingsrichting.
Het is misschien aardig om te weten dat dit effect pas beschreven werd in 1959
(door J.Terrell), terwijl de speciale relativiteitstheorie al van 1905 dateert!
De uitwerkingen van deze opgaven staan beschreven in het collegedictaat
Speciale Relativiteitstheorie.
Maar natuurlijk eerst zelf de opgaven maken. Volg daarna de links voor
opgave 1
(hoofdstuk 4),
opgave 2
(paragraaf 4.2) en
opgave 3
(paragraaf 6.3). Je zult zien hoeveel voldoening het geeft dat je dat allemaal
eerst zelf hebt kunnen "ontdekken". Dat is waarom natuur- en sterrenkunde zo
leuk is.
Deze opgaven werden door Arjan
Keurentjes samengesteld in het kader van een "werk-proefcollege" bij
het proefcollege relativiteitstheorie,
afgestemd op leerlingen van 5 en 6 VWO. Je kunt op de
Web-pagina meer informatie vinden
over de speciale relativiteitstheorie, en het eerstejaarscollege natuur-
en sterrenkunde dat hieraan gewijd is.

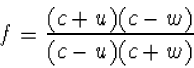
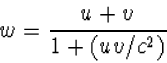
![]() met de gezichtslijn.
met de gezichtslijn.
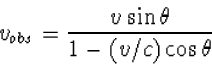
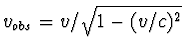 .
.
