
|
I am a postdoctoral research scientist in the Soft Matter Theory Group at the Instituut-Lorentz for theoretical physics, Leiden University. I am interested in the mechanics and statistical mechanics of soft materials. In the past few years, I have studied the mechanical response of slender elastic rods, plates, and shells, focusing on the effects of inhomogeneity and stochastic fluctuations. I'm currently interested in using similar ideas to describe biological systems including virus shells, the bacterial cell wall and mammalian muscle tissue, as well as strongly disordered elastic systems such as granular packings. A related theme is to use mappings and analogies from condensed matter systems to design mechanical metamaterials. Previously, I was a graduate student in the Applied Physics Ph.D. program at the Harvard School of Engineering and Applied Sciences in the research group of Prof. David R. Nelson. An electronic version of my thesis is available here. I graduated from Princeton University in 2007 with an undergraduate degree in Physics and certificates in Engineering Physics and Applications of Computing. You'll find more details in my CV. |

|
Research
Topological mechanical metamaterials
|
Topological phases of electronic matter display robust conducting edge states that are protected against disorder. A recently discovered mapping between lattices of balls connected by springs and topological electronic insulators revealed the possibility of analogous protected edge motions in mechanical systems. We exploit these topological mechanical lattices to introduce localiezed mechanical motion at specific points in an otherwise rigid lattice, and to sculpt buckling zones in lattices of flexible beams that fail preferentially under uniform external stresses. |

|
Papers:
Topological modes bound to
dislocations in mechanical metamaterials,
Nat. Phys. 11, 153 (2015).
[PDF][arXiv][videos]
(Chosen for the cover
of the February 2015 issue of Nature Physics, and with an accompanying commentary.)
Selective buckling via
states of self-stress in topological metamaterials,
PNAS 112, 7639 (2015).
[PDF][arXiv][videos]
Defects and differential growth in cylinders
|
Gram-negative bacteria have a cell wall composed of a peptidoglycan mesh that is only a single molecule layer thick, yet withstands a significant internal pressure. The addition of new material to the cell wall can be modeled by the motion of defects within this mesh. The elastic stresses induced by these defects have important consequences for the dynamics of growth as well as the stability of the cylindrical shape. We use the theory of dislocations and differential geometry, along with numerical simulations, to investigate the shape and growth of pressurized cylinders with defects and added material. |
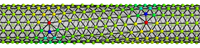
|
Paper:
Theory of interacting
dislocations on cylinders,
Phys. Rev. E 87, 042314 (2013). [PDF]
Crystal growth on curved surfaces
|
Regular crystals with triangular or honeycomb lattices can be readily formed on planar surfaces. Attempt to form the same crystal on a curved surface, such as the surface of a sphere, and it is forced to stretch or introduce defects in its perfect structure to accommodate the underlying curvature. How does a crystal grow under such constraints? Can it evade topological defects? Beautiful experiments involving colloidal crystallization on droplet surfaces from the Manoharan lab suggest that the answer might lie in growing branched, ribbon-like crystals, inspiring a theory of anisotropic crystal growth on curved surfaces. |

|
Paper: Elastic instability of a crystal growing on a curved surface, Science 343, 634-637 (2014).
Buckling of inhomogeneous elastic shells
|
Apply a large enough pressure on the walls of a hollow sphere, and it buckles inward. This elastic instability of thin spherical shells can be observed on scales ranging from the Astrodome to ping-pong balls to viral capsids. We studied how the well-known instability is modified by inhomogeneities in the shell thickness, whether a gradual change in thickness or a localized soft region in an otherwise uniform shell. Thinner regions control the buckling behaviour, but sometimes in unexpected ways, with important consequences for the reversibility and imperfection sensitivity of the buckling transition. |

|
Papers:
Buckling pathways in spherical
shells with soft
spots, Soft Matter 9, 8227 (2013). [PDF]
Delayed
buckling and guided folding of inhomogeneous capsules,
Phys. Rev. Lett. 109, 134302 (2012). [PDF]
Thermal fluctuations in thin elastic shells
|
The rigidity of a thin elastic sheet falls dramatically with decreasing thickness. Thin membranes and shells with thicknesses at the nanoscale are floppy enough to exhibit deformations purely due to thermal fluctuations. Such membranes may be considered the two-dimensional equivalent of polymers: their mechanical response is strongly influenced by entropy. In particular, the elastic constants associated with deformations (the bending rigidity and the stretching, or Young's, modulus) acquire thermal corrections. We calculated the effect of thermal fluctuations on spherical shells, taking into account the effects of curvature and a pressure difference between the inside and outside. Our results have consequences for interpreting the mechanical response of microcapsules and red blood cells. |

|
Paper: Fluctuating shells under pressure, Proc. Natl. Acad. Sci. USA 109, 19551 (2012). [PDF]
Lattice models of self-organization
|
The controlled manipulation of structures on the micro- and the nanoscale is a challenge with implications for nanotechnology. Capillary forces have been exploited to induce elastic microstructures to self-organize into ordered arrays. In collaboration with the Aizenberg Lab at Harvard, we borrowed a model of surface deposition of particles called cooperative sequential adsorption to understand the appearance of highly ordered patterns in arrays of flexible microfibers attached to a substrate. Our model showed that near-neighbor-like interactions between clusters of pillars were sufficient to explain the long-ranged ordering and accounted for the specific statistics of domain walls observed in experiments. |

|
Paper: Two-parameter sequential adsorption model applied to microfiber clustering, Soft Matter 6, 2421 (2010). [PDF]
Jayson Paulose. Updated 2013/10/09. CSS Template from www.styleshout.com.